「多変量解析のはなし」を読んで。
もっと詳しく書こうと思ったが、図や数式を書くのに挫折したので、できるかぎりで。
まずは、2つの変数の関係を表すところから。例えば…数名の、1週間に肉を食べる回数と、体重とのデータがあったとする。x軸に体重を、y軸に肉を食べる回数をとって、1名ごとに書き入れると、下図のようになる。
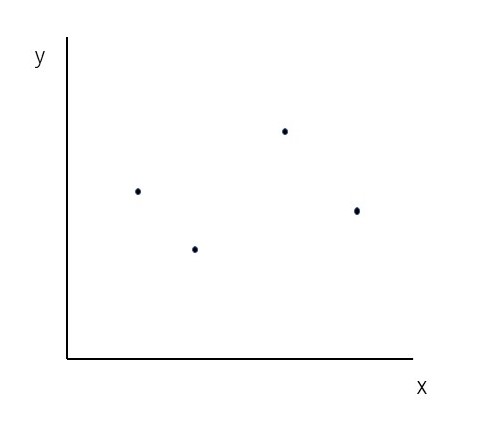
なんとなく、右肩上がりにみえなくもないような…しかし、人間の予想で直線を書き入れるのは失敗のもと。はっきりと、これだ!という直線を引くにはどうしたらよいか?
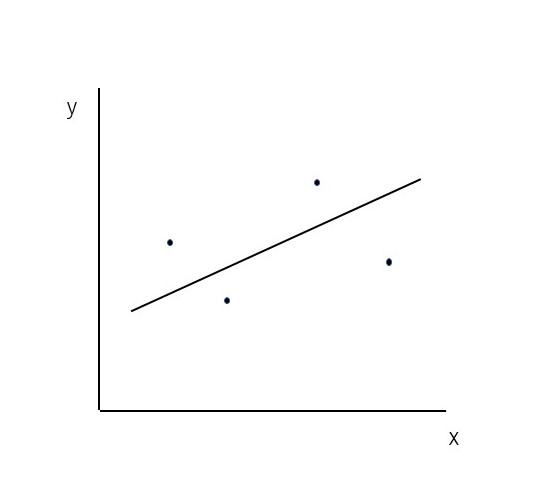
上図のように、いくつかの点の配列を1本の直線で代表することを直線回帰という。
余談:ふつうの日本語の感覚でいくと、回帰というと、「原点回帰」のように、ひとめぐりして戻ってくる、というイメージだが、統計用語でなぜここに「回帰」が出てくるのか。それは、進化論で有名なダーウィンの弟子であるFrancis Galtonが言い出したと言われている。Galtonは、親が高身長なら子も高身長、親が低身長なら子も低身長…というように、親と子の身長には45度近い傾きをもつ直線的な関係があると信じていた。しかし実際に調べてみると、高身長の親からはそれほど高身長の子は生まれず、低身長の子からはそれほど低身長の子は生まれない…というように、子供たちの身長は平均値のほうへ帰ってしまっていた。そのため、親と子の身長の関係は、当初Galtonが思っていたよりも傾きの緩やかな直線で表されることとなった。この現象をみて、Galtonはこの直線を回帰直線と名付けたのだそうな。…こういう、言葉の由来がわからないと、そこで止まってしまって先が頭に入らない…文系あるあるかな?余談終わり。
回帰直線を科学的に求める方法を以下に述べる。いくつかの点の傾向をなるべく忠実に代表するような直線(y=ax+b)と、実際の点との距離を、下図のようにεで表してみる。

仮に、一番左端の点、つまり(x1, y1)の点がこの直線上にあるなら、y1=ax1+bのはずだが、実際はそれよりもε1だけ上方にずれている。すなわちy1=ax1+b+ε1となる。したがって、ε1=y1-ax1-bとなる。この関係を一般化すると、εi=yi-axi-bということ。
εiの和が最も小さくするようにすれば、各点からの距離が最も短い直線、すなわちこれらの点の傾向を代表する直線となる。
ここから先は数式ごにょごにょなので割愛するが、∑εi2=∑(yi-axi-b)2が最小になるようなaとbを求めることができる。
では、変量が3つに増えた場合はどうなるか?その場合は、回帰直線でなく、回帰平面を求める方法となる。下図のようにイメージして、εの和が最小となるようなa、b、cを求める。
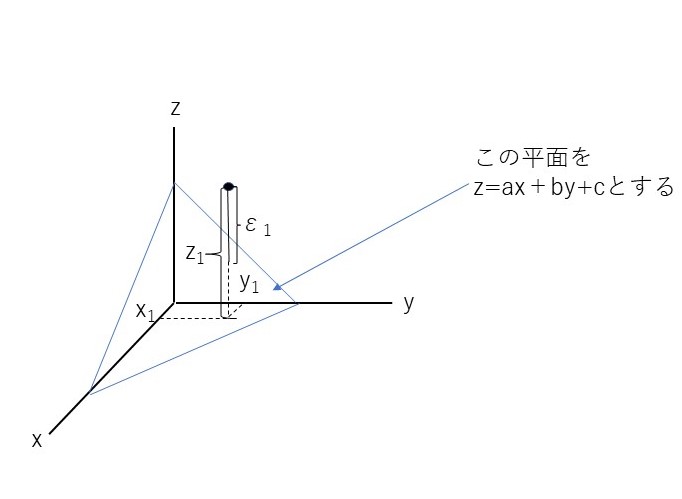
さらに変数が増えて4つなら、x、y、zによるwの回帰方程式はw=ax+by+cz+dとおいて、これまでと同じ手順をふめば、計算は面倒だがa、b、c、dを求めることができる。5つでも、6つでも…。
このように、2つ以上の変量を混ぜ合わせて1つの変量を回帰することを重回帰という。さきほどの、2つの変量を混ぜ合わせて1つの変量を回帰する(平面を使って)のを平面回帰といい、重回帰の一部。

